Binarized Network

Binarized Network

前向传播

把一个正常的NN，所有参数全部二值化，即torch.sign，大于等于0的浮点数全部变成1，否则全是-1；然后输入的样本也同样二值化。

这时，在进行前向传播时，【做矩阵乘法，对应元素相乘，最后再相加】的这一过程，转换为【对应元素做XNOR操作，然后POPCOUNT操作】。对应点做XNOR的操作是在模拟元素相乘这一步骤，由于都是±1，可以转为逻辑操作；POPCOUNT操作是统计某个向量有多少个1（比如一个向量由5个0和3个1构成，那么POPCOUNT操作结果就是3）

由于POPCOUNT结果一定是一个正数，下一层如果继续sign一定是1，所以通常选取一个threshold，大于这个门槛为1，否则为-1

反向传播

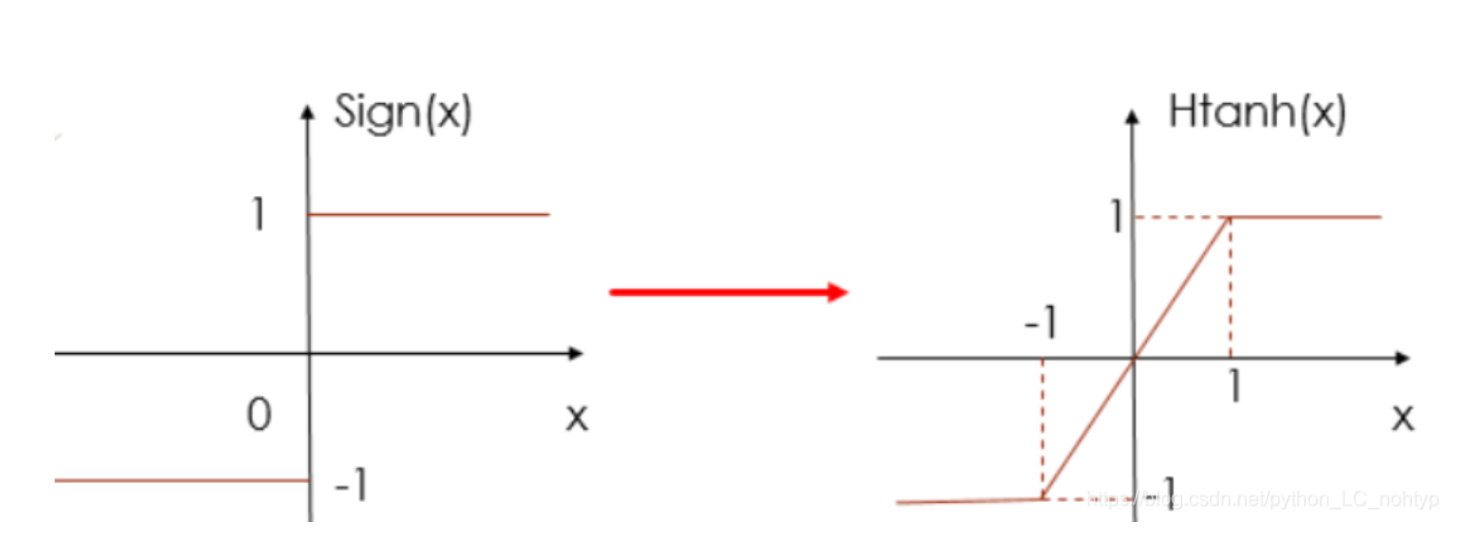
由于一开始有一个sign函数 $q=sign(r)$ ，loss对模型参数求梯度的时候，$\frac{\partial q}{\partial r}$ 梯度一定为0，没法用传统方法求梯度。所以把sign函数近似成Htanh函数。

$Htanh(x)=Clip(x,-1,1)=max(-1,min(1,x))$函数长这个样子：

求导就转化成了$\frac{\partial \text { loss }}{\partial r}=\frac{\partial \text { loss }}{\partial q} \frac{\partial H \tanh }{\partial r}$

这样在$r\in [-1,1]$区间内，就有了梯度，梯度是1，其余地方梯度还是0

(抄自 https://segmentfault.com/a/1190000020993594)

input = torch.randn(4, requires_grad = True)
output = torch.sign(input)
loss = output.mean()
loss.backward()
input
tensor([ 0.9303, -1.2768,  0.0069, -0.0968], requires_grad=True)
input.grad
tensor([0., 0., 0., 0.])

直接算梯度都是0，修改一下

class LBSign(torch.autograd.Function):
	@staticmethod
	def forward(ctx, input):
        return torch.sign(input)
    @staticmethod
    def backward(ctx, grad_output):
        return grad_output.clamp_(-1, 1)

sign = LBSign.apply
params = torch.randn(4, requires_grad = True)                
output = sign(params)
loss = output.mean()
loss.backward()       

params.grad
tensor(0.5000, grad_fn=<MeanBackward0>)

代码实现

参考自 https://github.com/itayhubara/BinaryNet.pytorch/tree/master，是论文作者写的一个pytorch实现

首先是二值化的函数

class Binarize(InplaceFunction):
    def forward(ctx, input, quant_mode='det', allow_scale=False, inplace=False):
        ctx.inplace = inplace
        if ctx.inplace:
            ctx.mark_dirty(input)
            output = input
        else:
            output = input.clone()
        scale = output.abs().max() if allow_scale else 1
        if quant_mode=='det':
            return output.div(scale).sign().mul(scale)
        else:
            return output.div(scale).add_(1).div_(2).add_(torch.rand(output.size()).add(-0.5)).clamp_(0,1).round().mul_(2).add_(-1).mul(scale)

    def backward(ctx, grad_output):
        # STE
        grad_input = grad_output
        return grad_input, None, None, None

作者的这个实现首先比较疑惑的一点是，要取sign之前是否除一个scale（正数）有什么影响吗？

然后这个backward中的STE实现，确实在(-1,1)之间STE是y=x函数，但这样写真的对吗？

参数和input的二值化：

class BinarizeLinear(nn.Linear):
    def __init__(self, *kargs, **kwargs):
        super().__init__(*kargs, **kwargs)

    def forward(self, input):

        input_b = binarized(input)

        weight_b = binarized(self.weight)
        out = nn.functional.linear(input_b, weight_b)

        if not self.bias is None:
            self.bias.org = self.bias.data.clone()
            out += self.bias.view(1,-1).expand_as(out)
        return out

class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.infl_ratio=3
        self.fc1 = BinarizeLinear(784, 2048*self.infl_ratio)
        self.htanh1 = nn.Hardtanh()
        self.fc2 = BinarizeLinear(2048*self.infl_ratio, 2048*self.infl_ratio)
        self.htanh2 = nn.Hardtanh()
        self.fc3 = BinarizeLinear(2048*self.infl_ratio, 2048*self.infl_ratio)
        self.htanh3 = nn.Hardtanh()

    def forward(self, x):
        x = x.view(-1, 28*28)
        x = self.fc1(x)
        x = self.htanh1(x)
        x = self.fc2(x)
        x = self.htanh2(x)
        x = self.fc3(x)
        x = self.htanh3(x)
        return x

x = torch.randn((2,28*28), requires_grad=True)
y = model(x)
print(y)
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
loss = criterion(y, torch.tensor([0,0]))
loss.backward()
optimizer.step()